If you ’ve been in a book store in the last six months – or anairport , wait room or college lecture class – you ’ve probably seen someone star at a sudoku . Given its popularity , one might think it ’s some fresh type of erotica . But no , it ’s just a puzzle . It ’s a widespread , logic - based furore of a puzzle that is simple enough to suck you in and difficult enough to keep you hooked .
In this clause , we ’ll bump out what a sudoku puzzler entails , how to go about solving one and where the concept develop ( hint : It ’s not Japan . permit ’s get lead off .
Sudoku Basics
Sudoku ( or su doku ) is a secret plan of phone number – specifically , the number 1 through 9 – but it really is n’t about math . It ’s aboutlogic . Instead of 1 through 9 , you could use the first nine letters of the alphabet or a set of nine symbol , and it would be the same game .
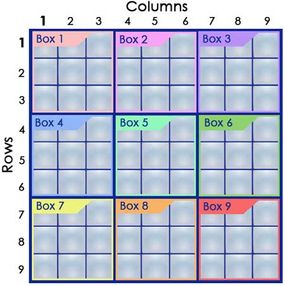
The basis of thesudoku gameis a nine - by - ninegrid . You ’ve got three sections to think about : rows , columnsandboxes .
The goal of sudoku is to fill each nine - square row , each nine - square column and each nine - solid box with the number 1 through 9 , with each numeral used once and only once in each section . It ’s theinteractionbetween the rows , columns and boxes that tells you where the number need to go . So if you were to start with a vacuous storage-battery grid and meet in the numbers for row 1 , tower 2 and boxwood 4 according to the sudoku rules , it might count something like this :
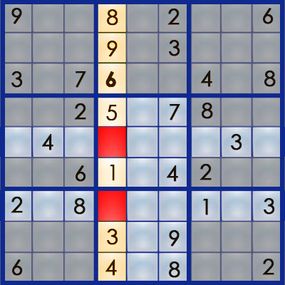
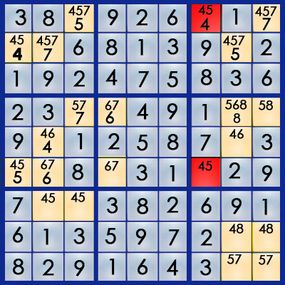
Of of course , starting with a blank grid would n’t make it much of a challenge . A sudoku puzzle already has some of the numbers filled in , and it ’s your job to figure out where the rest of the numbers go . Here ’s an representative of a real sudoku teaser from Michael Mepham ’s " Book of Sudoku 3 " :
Sudoku has several point of trouble , from easy to very severely , based on how many numbers you get to start with and where those numbers are position . ( Michael Mepham , mystifier creator for London’sDaily Telegraph , rates his puzzles as either docile , Moderate , Tough or Diabolical . ) An easy mystifier give you enough routine placed in enough strategic positions to allow you to find oneself the answer using fairly bare logic . Each puzzle has onlyone result .
The best elbow room to pick up the art of sudoku is by working through a mystifier . Let ’s take the air our way through the easy teaser above to get a flavor for the outgrowth . If you may solve an easy mystifier , you may figure out a hard one – it ’ll just take you more time .
Solving a Sudoku: Simple Logic
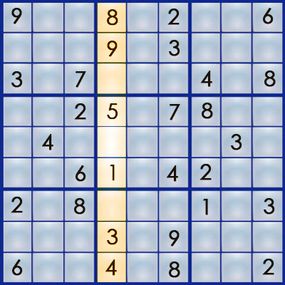
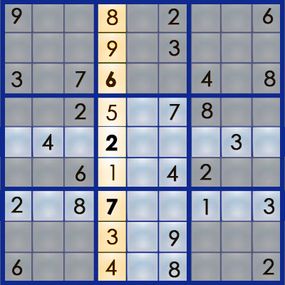
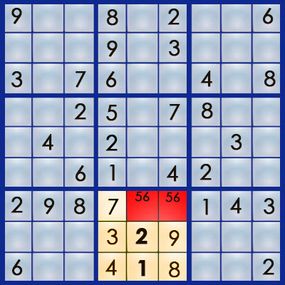
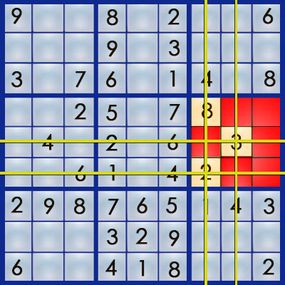
There is no right blank space to start a sudoku puzzle . you’re able to close your eyes and put your finger on the puzzle and start there , and that ’s as right a place as any . Probably the most lucid place to start , though , is at a rowing , tower or corner that has a lot of number in it . rent ’s take a look at the puzzle from the previous page :
Columns 4 and 6 each have six numbers filled in . rent ’s embark on the mystifier at column 4 , which already has its 1 , 3 , 4 , 5 , 8 and 9 .
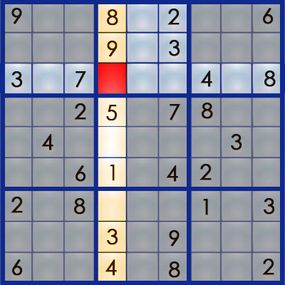
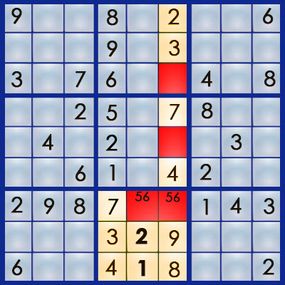
In parliamentary law to have one and only one of each figure from 1 to 9 , we ’re expire to have to put up column 4 with its 2 , its 6 and its 7 . But we ca n’t just put them anywhere – each identification number has a specific location in the puzzler ’s response . So where does each routine go ? To find out , we need to look at the rows and box that interact with column 4 . Take a feeling at the empty foursquare at dustup 3 , pillar 4 ( 3,4 ) , and the row and loge that interact with it :
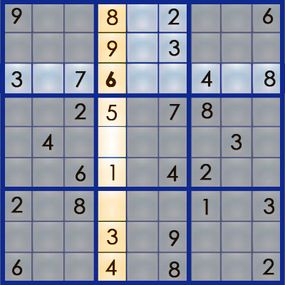
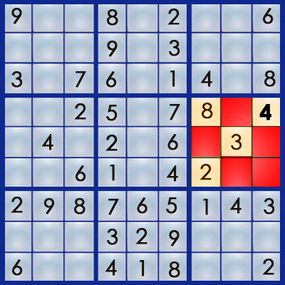
The " unsubdivided system of logic " approach to sudoku require only visual analytic thinking and goes something like this : Can the 2 go in the empty square toes ? It ca n’t , because box 2 already has a 2 , and it can only have one of each turn . Can the 7 go there ? wrangle 3 already has its 7 , so we ca n’t put a 7 there , either . That leaves us with the 6 . Neither row 3 nor box 2 already has a 6 , so we acknowledge the 6 is correct for that cell . We ’ve solve our first number !
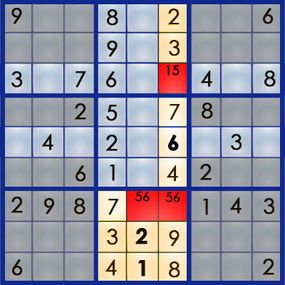
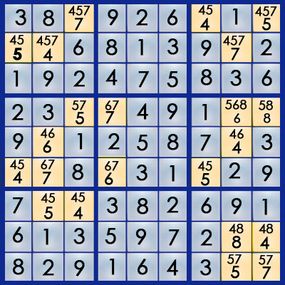
Now let ’s work out the rest of column 4 , which still needs its 2 and its 7 . The empty square at 5,4 interacts with rowing 5 and box 5 , and the empty square at 7,4 interacts with run-in 7 and box 8 .
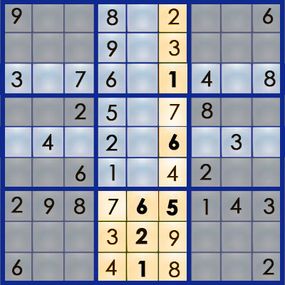
Since box 5 already has its 7 , we ca n’t put a 7 in the 5,4 square . So properly there we know the 2 goes at 5,4 , and the 7 must go at 7,4 :
We ’ve now work all of pillar 4 , and we used only simple logic to do it . Since this is an easy mystifier , we could likely resolve a good portion of it this way of life . But it ’s not always so clear - cut . There are strategies we can expend when the solution is not so obvious , and it all take up with some piddling pencil marks .
Solving a Sudoku: Possible Numbers
pencil in possible solvent for empty second power becomes of the essence as sudoku puzzles get toilsome . But you ’re not venture when you pencil in . You ’re simply name the potential solution . You should n’t approximate at sudoku – it ’ll in all probability end up messing up the entire puzzler so that you have to start all over , because everything is interconnected .
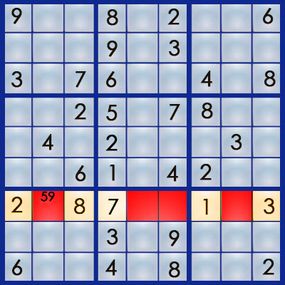
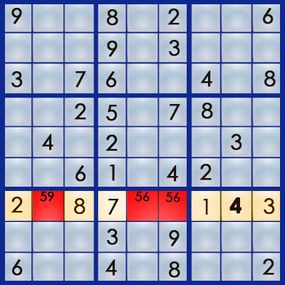
By penciling in all of the potential number for each square in a given row , column or boxwood , we can employ certain strategies to solve the section . Let ’s face at dustup 7 , which has four empty square and needs a 4 , a 5 , a 6 and a 9 .
We ’re going to pencil in all of the numbers that could peradventure lick each empty square , severally . So , of the numbers 4 , 5 , 6 and 9 , which could peradventure reset the square at 7,2 ? The 4 ca n’t go there , because column 2 already has a 4 . The 5 is a possibility , because neither row 2 nor box seat 7 has a 5 yet . The 6 is out because box 7 has a 6 already . The 9 could go there , because row 2 and corner 7 are both missing a 9 . So we ’re going to pencil in " 5 9 " for the public square :
Using the same unconscious process for the second power at 7,5 , we can eliminate the 4 and the 9 ( box 8 already has one of each ) and pencil in a 5 and a 6 . For the square at 7,6 , we can pencil in a 5 and a 6 . And for the square at 7,8 , any of the phone number will work on :
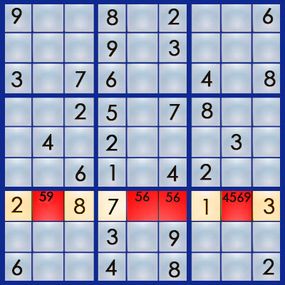
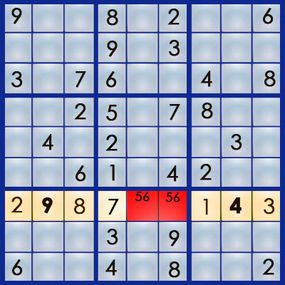
wait at the numbers you ’ve pencil in , you ’ll notice two things : First , two of the squares have the same pair of number ( and only those two numbers ) , and second , the 4 only appear once . Let ’s start with the 4 that only come along in square 7,8 . Using what we ’ll call the " single occurrence " strategy , we bang that if the only seat a 4 can go is in 7,8 , we ’ve solved that second power , because row 7 want a 4 . So now , quarrel 7 looks like this :
Now , let ’s look at the repeating duad : Both 5 and 6 – and only 5 and 6 – can go in square 7,5 and 7,6 . What we ’ve capture here is a set of matching brace . The 5 must go in one of those two squares , and the 6 must go in one of those two squares . Using thematching pairsstrategy , we can now egest the 5 from the square at 7,2 , because we know it does n’t go there . We ’ve solve another square :
By the path , the " matching pair " elimination strategy also works as " matching triad , " where you have three squares with the same triad of numbers , andonlythat trio of numbers game , in each square .
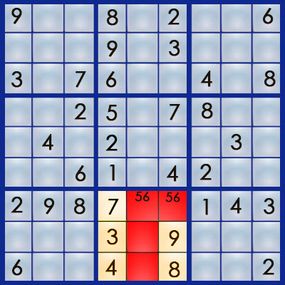
From what we ’ve penciled in so far , we still do n’t know which square gets the 5 and which gets the 6 , so we ’ll pencil in some more issue . get ’s see what we can do with box 8 , which has four empty squares and needs its 1 , 2 , 5 and 6 .
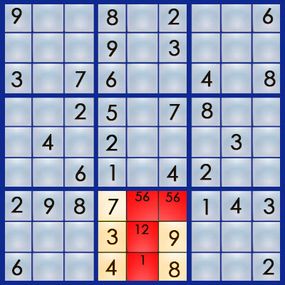
Two of those squares are already pencil in with a pit pair of 5 and 6 , so we recognize we can eliminate 5 and 6 as possible root for the other boxes . That leaves us with 1 and 2 . Either one of those numbers pool could work out the foursquare at 8,5 – neither row 8 nor column 5 has a 1 or a 2 . But row 9 has a 2 , so we ca n’t pencil in a 2 for the 9,5 foursquare . Here ’s what we ’ve got :
remark anything ? There ’s only one number in the 9,5 lame . Using what Mepham dubs thelone numberstrategy – probably the simplest strategy in sudoku – we know that 1 is the resolution at 9,5 . And since the 1 for boxwood 8 is at 9,5 , we can eliminate the pencil - in 1 from the square at 8,5 , allow for only a 2 – and another resolve foursquare .
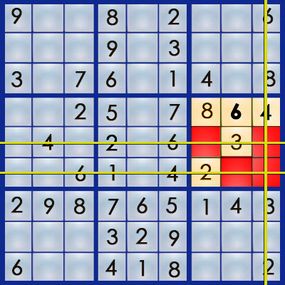
But we still do n’t know the right attitude for the 5 and the 6 . Solving editorial 6 will tell us which number solves the public square at 7,6 . We have three empty squares in pillar 6 , one of which is already penciled in with all of its possible solutions :
Column 6 postulate a 1 , a 5 and a 6 . For the square at 3,6 , 1 and 5 are theory ( course 3 already has its 6 ) . For the square at 5,6 , the only potential result is a 6 , because box 5 already has a 1 and a 5 .
We now know that the answer at 7,6 has to be the 5 , the solution at 3,6 has to be the 1 , and the solvent at 7,5 has to be the 6 .
Because the interaction between rows , columns and box is the whole point in sudoku , solve a individual square can in a flash show you five other solutions . Up to now , we ’ve used uncomplicated logical system and we ’ve looked for possible numbers for a given second power . In the next section , we ’ll practice another approach : wait for potential squares for a yield number .
Solving a Sudoku: Possible Squares
This time , instead of looking for the correct identification number for a square toes , we ’re going to search for the right second power for a issue . To do this , we ’re going to draw in some lines . Take a look at box 6 :
Box 6 needs a 4 . have ’s bump out where it goes by eliminating all of the box where it ca n’t go . There ’s a 4 in row 5 , so we ’ll trace a product line through that dustup . There ’s also a 4 in row 6 and column 7 and 8 . We ’ll suck lines through all of those .
Now there ’s only one open square toes in box 6 – the square at 4,9 . We ’ve solve the 4 .
Let ’s draw some more lines to find out the positioning of the 6 . We can strike through row 5 , quarrel 6 and editorial 9 , leaving only one open square . We can put the 6 in the square at 4,8 .
You now have all the knowledge you require to stop the puzzle yourself !
Using dewy-eyed logic and the basic scheme we ’ve discussed here , along with the thousands of other strategies out there develop by sudoku enthusiast , you ’ll be able to puzzle out just about any sudoku puzzle . As the difficultness increases , it ’ll just take you longer to resolve each hearty because some square wo n’t be solvable until you ’ve solved certain other square – sometimes until you ’ve solved entire regions of the grid . As you work on more puzzles , you ’ll come up with your own approaches and strategy . It ’s all a matter of finding and cultivating your own sense of sudoku logic .
While sudoku is a game of logic , there are some puzzles that at long last defy logic and require – to the horror of many sudoku purists – guessing .
Solving a Sudoku: Diabolical and Beyond
Until recently , some of Michael Mepham ’s hellish - rated sudoku in London’sDaily Telegraphcould not be clear by system of logic alone . They in reality required pretend at a certain distributor point , which sudoku purist consider a real no - no . Due to the amount of controversy ( and hate mail ) Mepham received , he has stopped write puzzles that need guessing . Still , the physical process of solving one of these puzzles is interesting , if only because you have to know enough to be perfectly certain there are no more clues before you start out the guessing process . Mepham called the scheme " Ariadne ’s Thread " ( see below ) , which entail pick one of two possible solutions for a fall in square and watch over it until you progress to a solution or a idle end . If you reach a all in end , you retrace your step to the guessing point and pick a unlike number .
In Michael Mepham ’s " Book of Sudoku 3 , " there ’s a diabolical sudoku that protrude like this :
Using logic , you may get here :
But there are no more ordered clues – we ’re stuck . The only alternative give to us is to imagine – and leave our numbers pencil in so we can follow Ariadne ’s Thread back to our start stage if our guess turn out to be wrong . If we choose one of the second power with only two options , we ’ve got a 50/50 fortune of foot the ripe number . Let ’s go to row 2 , column 1 and pick the 4 . Assuming that 4 is the solution to the 2,1 square , we can clear a bunch of other squares by extension – but we end up with a problem .
If the resolution at 1,7 is a 4 , then the solution at 6,7 has to be the 5 . But row 6 already has a 5 . So now we need to erase the answer we describe from our guess and go back to hearty 2,1 . This prison term , we ’ll peck the 5 .
The 5 is indeed the solution to the square toes at 2,1 , and it allows us to solve the entire puzzler .
Although Mepham stopped publishing guess - necessary sudokus in his column , you may still access them at Mepham ’s sudoku Web site , sudoku.org.uk .
In response to the awful popularity of sudoku , different versions of the mystifier have emerged to render even more of a challenge . One type of " utmost sudoku " is3 - five hundred sudoku . Just delineate up nine unadulterated sudoku gridiron into a three - dimensional block that necessitate complete rows , columns and boxes on three interconnected axes , and you ’ve scram yourself a 3 - D sudoku mystifier . All of the same rule give , but now you ’re cultivate on multiple planes . To work out the cube , you need to do work out the solutions for each of the nine grid individually , although if you download one of the dozens of 3 - five hundred sudoku computer programs , you could cultivate on the mystifier in full 3 - D glory .
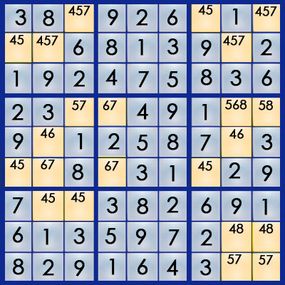
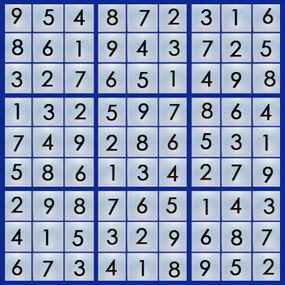
Puzzle Answer from Previous Page
For more information on sudoku and related to topics , contain out the links on the next page .